質問＜５９６＞２００１／８／１０
from=まり
「２次関数」

問１
不等式x2乗－(a+1)x+a＜0を満たす整数がちょうど2個だけあるような
実数ａの値の範囲を求めよ。

問２
放物線y=x2乗+2kx+4とｘ軸が共有点をもたないとき、自然数ｋの最大値
を求めよ。

お返事２００１／８／１１
from=武田

問１
ｘ2 －（ａ＋１）ｘ＋ａ＜０
（ｘ－１）（ｘ－ａ）＜０
１とａの大小によって、次の２つの場合に分かれる。


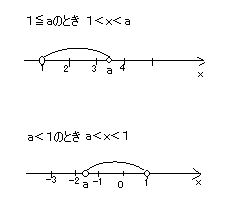
したがって、
この範囲内に整数が２個取れるのは、ａの範囲が次の場合である。
－２≦ａ＜－１または３＜ａ≦４………（答）

問２
ｙ＝ｘ2 ＋２ｋｘ＋４がｘ軸と交点を持たないということは、
判別式Ｄ＜０より、
Ｄ／４＝ｋ2 －４＜０
（ｋ－２）（ｋ＋２）＜０
－２＜ｋ＜２
自然数の最大は、
∴ｋ＝１………（答）