複素数平面上で、複素数αは2点 1 + i と
1 - i とを結ぶ線分上を動き、複素数β
は原点を中心とする半径1の円周上を動くものとする。
(1)α + β が複素数平面上を動く範囲の面積は、
□ + □π である。
(2)αβ が複素数平面上を動く範囲の面積は、□πである。
(3)α^2 が複素数平面上で描く曲線と虚軸で
囲まれた範囲の面積は □ である。
□内をもとめよ。
(1)
α=1+ki(-1≦k≦1)
β=cosθ+isinθ(0≦θ<2π)
とすると、
α+β=(1+cosθ)+i(k+sinθ)
これがどのような図を描くかは、実部をx、虚部をyとおいて、
{x=1+cosθ
{y=k+sinθ
変形して、
{(x-1)=cosθ
{(y-k)=sinθ
2乗して足すと、
(x-1)2 +(y-k)2 =cos2 θ+sin2 θ=1
-1≦k≦1の範囲でkを変化させ図を描くと、
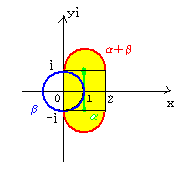
図より、面積は
2×2+π(1)2 =4+π………(答)
(2)
αβ=(1+ki)(cosθ+isinθ)
=(cosθ-ksinθ)+i(kcosθ+sinθ)
{x=cosθ-ksinθ
{y=kcosθ+sinθ
2乗して、
{x2 =cos2 θ-2ksinθcosθ+k2 sin2 θ
{y2 =k2 cos2 θ+2ksinθcosθ+sin2 θ
足すと、
x2 +y2 =(1+k2 )cos2 θ+(1+k2 )sin2 θ
=(1+k2 )(cos2 θ+sin2 θ)
=(1+k2 )・1
=1+k2
-1≦k≦1の範囲でkを変化させ図を描くと、
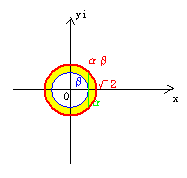
図より、面積は
π(\(\sqrt{\quad}\)2)2 -π(1)2 =2π-π=π………(答)
(3)
α2 =(1+ki)2
=(1-k2 )+2ki
{x=1-k2
{y=2k
1
k=―yを代入して、
2
1
x=1-(―y)2
2
-1≦k≦1より、-2≦y≦2
図を書くと、横に寝た放物線だから、
1
x=-―y2 +1
4
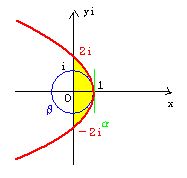
虚軸で囲まれた部分の面積は、積分で、
2 1
∫ (-―y2 +1)dy
-2 4
1 2
=[-――y3 +y]
12 -2
8 8
=-――+2-(――-2)
12 12
16 32 8
=4-――=――=―………(答)
12 12 3