１）は
　　　　　　　　　\(\frac{1}{2}\)
　　　\(\sqrt{\quad}\)ｘ　　　ｘ
ｙ＝ｘ　　　＝ｘ

２）は
　　　　２
　　　ｘ
ｙ＝ｘ

より、

ｙ＝ｘ＾（ｘ＾ｎ）のグラフで、
１）はｎ＝１／２＝０．５
２）はｎ＝２
のときにあたるから、
コンピュータを使った作図より、



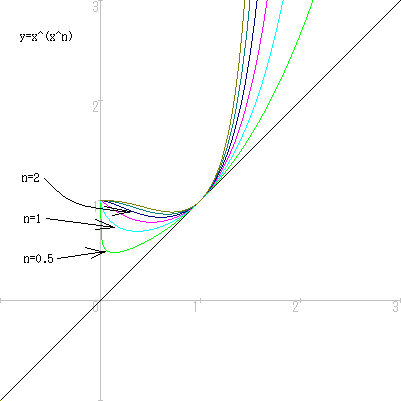
両方とも極限値は１となるが、

解き方について、ｄ３さんとHoshinoさんからからアドバイスをいただきました。
感謝！！

lim(x→+0)\(x^{x}\)を考えましょう．
y＝\(x^{x}\)　（＞0 ）の両辺に対し自然対数をとり
　log(y)＝x・log (x) ＝ log (x) ／(\(\frac{1}{x}\))
ロピタルの定理を適用し，極限はx→+0として

lim｛log(y)｝＝lim {log (x) ／(\(\frac{1}{x}\))}＝lim｛(\(\frac{1}{x}\)) ／(－1/\(x^{2}\))｝
＝lim｛－x｝＝－0
したがって，lim(y) ＝lim｛\(x^{x}\)｝が有限確定値を持つとき，
その値は lim｛\(x^{x}\)｝＝exp(－0) ＝ 1

log{x^(\(\sqrt{\quad}\)x)}＝\(\sqrt{\quad}\)xlogx＝｛2\(\sqrt{\quad}\)x・log (\(\sqrt{\quad}\)x)｝→0　よって1です．

log{x^(\(x^{2}\))}＝\(x^{2}\)logx＝x(xlogx)→0　です．よって1です．

ロピタルを使っていますので，そうでないと非常に長くなります．
どこかで読んだのですが，{\(\frac{1}{n}\)}で極限を考えて，
1/(n+1)≦x≦\(\frac{1}{n}\) ではさみうちです．

先ず lim_(x→+0) (x log x) = 0.
を証明する。

その為に x = e^(-t) と置くと, x→+0 の時 t → +∞.
x log x = -t e^(-t) = -t/\(e^{t}\)
だが,
\(e^{t}\) > 1 + t + (\(t^{2}\))/2, t > 0 (*)
が証明できるので
0＜ t/\(e^{t}\)＜ t/(1 + t + (\(t^{2}\))/2)→0 as t→+∞.
従って
lim_(x→+0) (x log x) = 0.

(*) を証明する。
f(t) = \(e^{t}\) - 1 - t - (\(t^{2}\))/2
と置く。 f(0) = 0.
f'(t) = \(e^{t}\) - 1 - t.
f'(0) = 0.
f"(t) = \(e^{t}\) - 1 > 0, t > 0
従って, f'(t) は狭義単調増加だから f'(t) > 0, t > 0.
従って f(t) も狭義単調増加だから f(t) > 0, t > 0.

さて
(1) だが (必要なら s = \(\sqrt{\quad}\)x と置き換えれば)
log x^(\(\sqrt{\quad}\)x) = (\(\sqrt{\quad}\)x) log x = 2(\(\sqrt{\quad}\)x) log (\(\sqrt{\quad}\)x)→0 as x→ +0.
即ち
x^(\(\sqrt{\quad}\)x) = e^(log x^(\(\sqrt{\quad}\)x))→1.

(2) も同様に
log x^(\(x^{2}\)) = \(x^{2}\) log x = x(x log x) → 0 as x → +0.
即ち
x^(\(x^{2}\)) = e^(log x^(\(x^{2}\))) → 1.