長さ2の線分ABを直径とする半円を考える。
円弧上の点Pに対して、∠PAB=θ(0°<θ<90°)とし、
△PABの周の長さをd、△PABの面積をSとする。
(1)dをθを用いて表せ。
(2)dを最大にするθの値を求めよ。
(3)Sをθを用いて表せ。
(4)S/dの最大値を求めよ。
質問が多いかもしれませんが、解説よろしくお願いいたします。
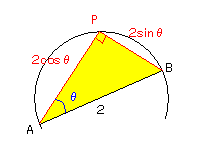
(1)d=2+2sinθ+2cosθ=2(1+sinθ+cosθ)………(答)
(2)d´=2cosθ-2sinθ=0より、
cosθ=sinθ
0°<θ<90°より、
∴θ=45°………(答)
(3) \(S=\frac{1}{2}\cdot 2\cos \theta \cdot 2\sin \theta =2\sin \theta \cos \theta =\sin 2\theta\) ………(答)
(4) \(\frac{S}{d}=\frac{\sin 2\theta }{2(1+\sin \theta +\cos \theta )}\) をθで微分して、
\((\frac{S}{d})^{\prime }=\frac{2\cos 2\theta \cdot 2(1+\sin \theta +\cos \theta )-\sin 2\theta \cdot 2(\cos \theta -\sin \theta )}{4(1+\sin \theta +\cos \theta )^{2}}\)
\(=\frac{4(\cos ^{2}\theta -\sin ^{2}\theta )(1+\sin \theta +\cos \theta )-4\sin \theta \cos \theta (\cos \theta -\sin \theta )}{4(1+\sin \theta +\cos \theta )^{2}}\)
\(=\frac{(\cos \theta -\sin \theta )(\cos \theta +\sin \theta +2\sin \theta \cos \theta +\sin ^{2}\theta +\cos ^{2}\theta -\sin \theta \cos \theta )}{(1+\sin \theta +\cos \theta )^{2}}\)
\(=\frac{(\cos \theta -\sin \theta )(\cos \theta +\sin \theta +\sin \theta \cos \theta +1)}{(1+\sin \theta +\cos \theta )^{2}}\)
\(=\frac{(\cos \theta -\sin \theta )(\cos \theta +1)(\sin \theta +1)}{(1+\sin \theta +\cos \theta )^{2}}\)
分子=(cosθ-sinθ)(cosθ+1)(sinθ+1)=0より、
cosθ=sinθより、θ=45°
cosθ=-1より、θ=180°
sinθ=-1より、θ=270°
0°<θ<90°より、
θ=45°
したがって、最大値は
\(\frac{S}{d}=\frac{\sin 90^{o}}{2(1+\sin 45^{o}+\cos 45^{o})}=\frac{1}{2(1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}})}\)
\(=\frac{1}{2(1+\sqrt{2})}\) ………(答)