円に内接する四角形ABCDにおいて，直線DAと直線CBとの交点をP，直線BAと直線CD
との交点をQとする。∠APBの二等分線と辺AB，DCとの交点をそれぞれE，Fとし，∠AQD
の二等分線と線分EFとの交点をRとおく。


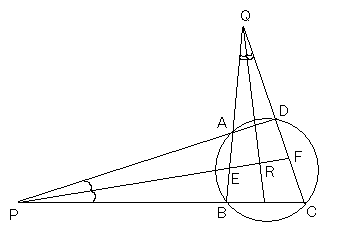
このとき，∠PRQ＝90°であることを示せ。


ガイドとして，QE＝QFの二等辺三角形をいえばよいとあるのですが
メネラウスの定理や角の二等分線と辺の比等思い当たる性質は利用しても
辺の比同士が複雑に絡んでいて過程が混乱してしまいます。
スマートな方法があると思うのですが，見当たらないのでお教え下さい。

★希望★完全解答★