問題：F=\(x^{2}\)/(x-1)の1＜xでの最小値mを求めよ
について。
F=x-1+1/(x-1)+2で相加相乗平均の関係よりx=2のときm=4
この解答は確かに正しいと思うのですが、
F=x+1+1/(x-1)で相加相乗平均の関係より、
x+1=1/(x-1)・・・☆が1＜xで解を持つとすると
(それをaとおく)x=aのときm=2\(\sqrt{\quad}\){(a+1)/(a-1)}・・・★
ここで☆の解はx=\(\sqrt{\quad}\)2(=a)なのでこれを★に代入して、
x=\(\sqrt{\quad}\)2のときm=2{(\(\sqrt{\quad}\)2)+1}
この解答はどうして答えが間違ってしまうのですか？
論理的にはあっていませんか？
★希望★完全解答★
＜質問＞８０２に、同様の疑問に対しての解答がありますので、
参照してください。
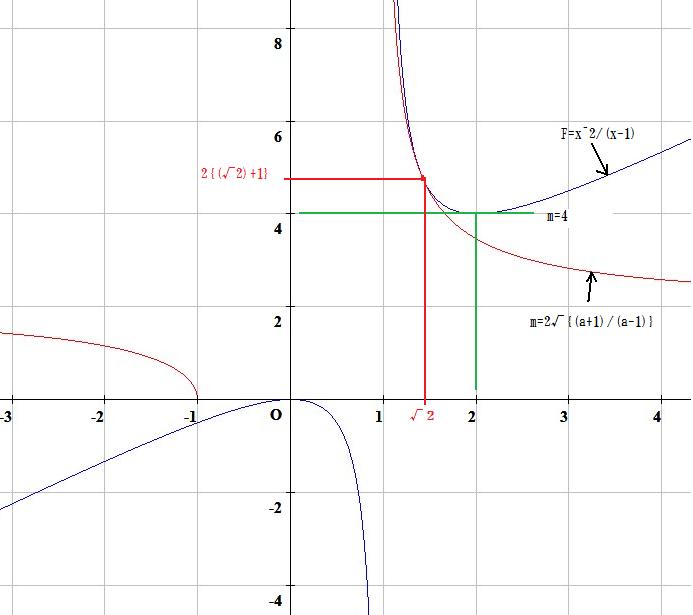
参考までに、グラフ化しましたので、違いが分かりますね。
こんばんは。武田先生の回答で納得できましたか？できたならよいのですが、少し補足して
おきます。
rotさんが書いた回答の二つ目はもちろん、論理的に間違っています。どこが間違いなのか、
分かったでしょうか。
二つ目の回答は、つまり、次のような内容です。
実数値関数、ｆ（ｘ）とｇ（ｘ）があり、
ある指定された範囲のｘに対しｆ（ｘ）≧ｇ（ｘ）、、、、（イ）
方程式ｆ（x）＝ｇ（x）は指定の範囲に解x＝ａを持つ、、（ロ）
この時、ｆ（ａ）はｆ（ｘ）の最小値である。、、、、（ハ）
「（イ）かつ（ロ）が成り立つ→（ハ）が成り立つ」が正しいと思いますか？
そんなわけはありませんね。ｆ（ｘ）が最小値を取るｘと、
方程式 ｆ（x）＝ｇ（x）の解ａが一致する保証はありません。
ただ、ｇ（ｘ）＝Ｃ＝一定 の時は話が別です。
この場合は
指定範囲のｘに対しｆ（ｘ）≧Ｃ (つまりｆの最小値はｃ以上）
であり、かつ
ｆ（ａ）＝Ｃ （つまりｆ（x）は実際に値Ｃを取る）
ですから、ｆ（x）の最小値は明らかにＣです。
つまり、下側の関数ｇ（x）（相加平均と相乗平均でいえば相乗平均）が、上側の関数ｆ（x）
（相加平均と相乗平均でいえば相加平均）の最小値を求めるのに役立つのは、ｇ＝定数の場合だけ。
普通は役に立たたず、定数の場合だけ例外的に役立つわけです。
納得できなければ、なんでも好きな関数のグラフを一つ描き、次に、最初に描いたグラフと
どこかで交わるけれど、上側にははみ出さないような別のグラフを描いてみて下さい。
２つ目のグラフは無数に描けて、交点が最小値になるとは全く限らないことがわかると思います。