問1
二つの2次方程式x2+ax+3a=0,x2-ax+a2-1=0について
(1) 少なくとも一方が解を持ちような定数aの値の範囲を求めよ。
(2)ともに解を持たないような定数aの値の範囲を求めよ。
問2
関数f(x)=ax2-4x+a-3(aは定数)が次の条件を満たすようなaの値の
範囲を、それぞれ求めよ。
(1)すべての数xに対してf(x)は常に正の値をとる。
(2)f(x)はあるxの値に対して正の値をとる。
(3)f(x)は正の値も負の値もとる。
問1
(1)
{x2 +ax+3a=0………①
{x2 -ax+a2 -1=0………②
解を持つのは、判別式D≧0のときだから、
①より、解を持つのは、
D=a2 -12a≧0
a(a-12)≧0
∴a≦0,12≦a
②より、解を持つのは、
D=a2 -4(a2 -1)≧0
3a2 -4≦0
(\(\sqrt{\quad}\)3a+2)(\(\sqrt{\quad}\)3a-2)≦0
2 2
∴-――≦a≦――
\(\sqrt{\quad}\)3 \(\sqrt{\quad}\)3
少なくとも一方が解を持つのは、(①がもつ)または(②がもつ)の
和集合となるから、
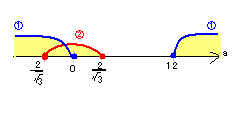
2
∴a≦―― ,12≦a………(答)
\(\sqrt{\quad}\)3
(2)
ともに解を持たないのは、(1)の逆だから、補集合より、
2
∴――<a<12………(答)
\(\sqrt{\quad}\)3
問2
(1)
f(x)=ax2 -4x+a-3において、
すべてのxの値に対して、f(x)が常に正とは、次のようなグラフの
時である。
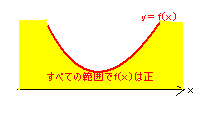
これは、下に凸より、a>0
x軸と交点がないから、判別式D<0より、
D/4=4-a(a-3)<0
a2 -3a-4>0
(a-4)(a+1)>0
∴a<-1,4<a
したがって、
4<a………(答)
(2)
あるxの値に対して、f(x)が正とは、次のようなグラフの時である。

これは、上に凸より、a<0
x軸と2つの交点があるから、判別式D>0より、
D/4=4-a(a-3)>0
a2 -3a-4<0
(a-4)(a+1)<0
∴-1<a<4
したがって、
-1<a<0………(答)
(3)
f(x)が正も負もとるのは、次のようなグラフの時である。
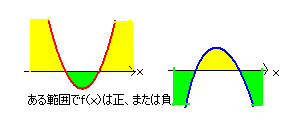
x軸と2つの交点があるから、判別式D>0より、
D/4=4-a(a-3)>0
a2 -3a-4<0
(a-4)(a+1)<0
∴-1<a<4
したがって、
-1<a<4………(答)