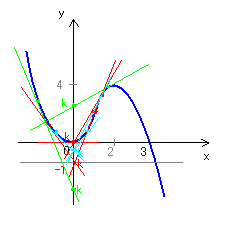
とある参考書に3次関数のグラフの接線は接点が異なると、
接線が異なるということから
接点の個数⇔接線の本数がいえる、
と言うようなことを書いてあったのですが、
どういうことでしょうか。
どうして接点の個数と接線の本数が等しくなるのか全く解りません。
よろしく御願いします。
d3さんとtoshiさんからアドバイスをいただき、そう言うことかと
合点しました。
「3次関数は、接点の個数と接線の個数が1:1で一致する」ことは、
d3さんが指摘の通り、「接点は連立の重解」のときだから、3次関数
は解3個の内2個が重解として使われるので、接線は1本しかないこと
が言える。
さて、質問の3次関数に対する接線の本数は、3次方程式の判別式によ
って求まる。質問<31>を参照。
\(y=-x^{3}+3x^{2}\) を微分して、
\(y\prime =-3x^{2}+6x\)
3次関数上の接点 \(P(t,-t^{3}+3t^{2})\) を通る接線の方程式は、
\(y-(-t^{3}+3t^{2})=(-3t^{2}+6t)(x-t)\)
この接線が点Q(0,k)を通るから、計算して
\(2t^{3}-3t^{2}-k=0\)
3次方程式ができる。
この方程式の解の個数が、接点の個数になるから、接線の本数にもなる。
(上記の接点の個数と接線の個数が1:1と一致するから)
3次方程式 \(x^{3}+mx+n=0\) の判別式は \(R=(\frac{n}{2})^{2}+(\frac{m}{3})^{3}\) より、
\(t^{3}-\frac{3}{2}t^{2}-\frac{k}{2}=0\)
\(t=s-\frac{p}{3}=s-\frac{-\frac{3}{2}}{3}=s+\frac{1}{2}\) と置き換えて、
\((s+\frac{1}{2})^{3}-\frac{3}{2}(s+\frac{1}{2})^{2}-\frac{k}{2}=0\)
\(s^{3}-\frac{3}{4}s-\frac{1}{4}-\frac{k}{2}=0\)
したがって、
\(m=-\frac{3}{4}\) より、判別式にあてはめて、
\(R=(\frac{n}{2})^{2}+(\frac{m}{3})^{3}=(\frac{-\frac{1}{4}-\frac{k}{2}}{2})^{2}+(\frac{-\frac{3}{4}}{3})^{3}\)
\(=(\frac{1}{8}+\frac{1}{4}k)^{2}-\frac{1}{64}=\frac{1}{16}k^{2}+\frac{1}{16}k=\frac{1}{16}k(k+1)\)
①R>0のとき、
k<-1,0<kで、1実数解2虚数解より、
接線は1本
②R=0のとき、 k=0,-1で、1実数解と重解より、
接線は2本
③R<0のとき、
-1<k<0で、3実数解より、
接線は3本